Deduplicating AI Thoughts at Scale: MinHash Fingerprinting in Practice
When your AI agent generates thousands of thoughts per hour, many of them start to look the same. Not identical — that would be easy to catch — but structurally similar: the same concepts rearranged, the same patterns with slightly different phrasing. We needed a way to detect this repetition in real time, at sub-second latency, without comparing every thought against every other thought.
This is the story of how we replaced 21 scattered similarity functions with a single MinHash fingerprinting module, and how it solved a problem we didn't know we had.
The Problem: Activation Saturation
Daimon is an autonomous AI agent with a cognitive loop that runs every 800 milliseconds. Each cycle performs spreading activation through an associative memory graph — concepts activate related concepts, and when enough activation converges, it triggers an LLM synthesis call.
The problem was subtle. Generic concepts like "market", "prediction", and "accuracy" appeared in nearly every thought. They saturated the activation map at the 1.70 ceiling, producing identical collisions every cycle. The LLM dutifully "synthesized" these noise collisions into profound-sounding but ultimately meaningless insights. We were paying for LLM calls to confabulate about noise.
We needed a gate: before triggering synthesis, check whether this combination of concepts is structurally novel or just the same pattern we've seen 50 times.
Why Jaccard Similarity
Jaccard similarity is the standard measure for set overlap:
J(A, B) = |A ∩ B| / |A ∪ B|
Two concept sets {market, prediction, crypto} and {market, prediction, accuracy} have a Jaccard similarity of 1/4 = 0.25 (one shared element out of four unique). Two identical sets score 1.0. Two disjoint sets score 0.0.
This is exactly the right metric for concept sets because:
- Order doesn't matter — concepts aren't sequential
- Duplicates are irrelevant — a concept is either present or absent
- Intuitive threshold — 0.65 similarity means "roughly two-thirds overlap"
The naive implementation is trivial:
def jaccard(set_a: set, set_b: set) -> float:
if not set_a and not set_b:
return 1.0
if not set_a or not set_b:
return 0.0
return len(set_a & set_b) / len(set_a | set_b)
But exact Jaccard has a problem: to compare a new thought against a window of 50 recent thoughts, you need 50 set intersection/union operations. As concept sets grow, this gets expensive. And if you want to compare against a longer history, the cost grows linearly.
Enter MinHash
MinHash (Min-wise Independent Permutations) was introduced by Andrei Broder in 1997 for detecting near-duplicate web pages at AltaVista (Broder, 1997). The core insight is that you can estimate Jaccard similarity without ever computing the actual intersection.
The theory rests on a beautiful property: if you apply a random hash function to every element in both sets and take the minimum hash value from each, the probability that the two minimums are equal is exactly the Jaccard similarity:
Pr[min(h(A)) = min(h(B))] = J(A, B)
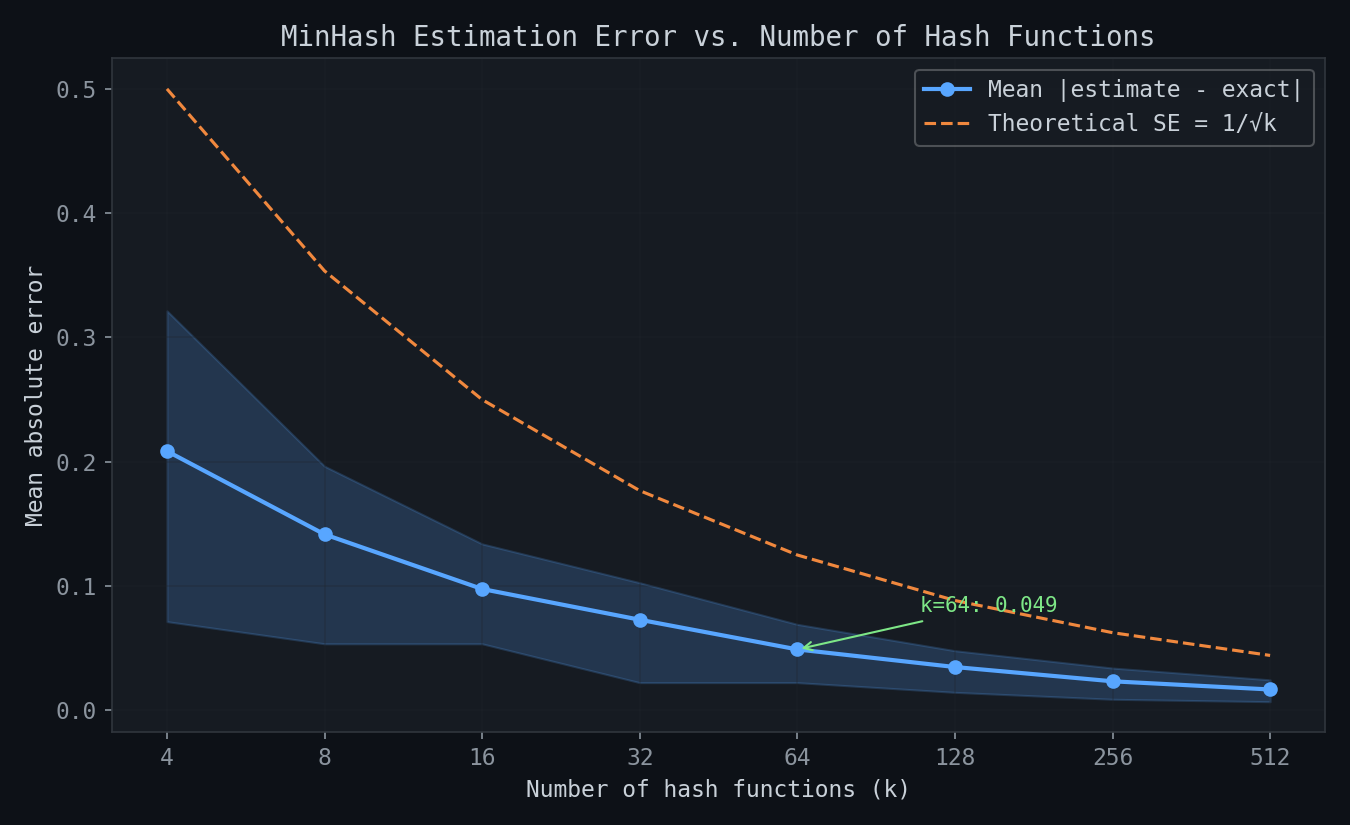
By using k independent hash functions and comparing the k minimums (the "signature"), you get an estimate of Jaccard with standard error 1/sqrt(k). With k=64 hash functions, the standard error is ~12.5% — good enough for a repetition gate, and much cheaper than exact computation.
The Universal Hash Family
Rather than generating 64 truly independent hash functions (expensive), we use the universal hash family:
h(x) = (a * x + b) mod p
where p is a large prime and (a, b) are random coefficients. This is a standard technique from Carter & Wegman, 1979, proven to provide pairwise independence — which is all MinHash requires.
We use the Mersenne prime 2^31 - 1 as p:
LARGE_PRIME = (1 << 31) - 1 # 2,147,483,647
Stable Hashing
A critical implementation detail: Python's built-in hash() is randomized per process (via PYTHONHASHSEED). Two processes hashing the same string get different results. Since Daimon runs as multiple systemd services sharing data, we need deterministic hashing:
def _stable_hash(s: str) -> int:
"""Process-independent 32-bit hash via md5 truncation."""
return int.from_bytes(
hashlib.md5(s.encode("utf-8", errors="replace")).digest()[:4],
byteorder="big",
)
MD5 is deterministic, fast, and we only need 32 bits. We're not using it for cryptographic purposes — collision resistance across the concept namespace is all we need.
The MinHasher Class
class MinHasher:
def __init__(self, num_hashes: int = 64, seed: int = 42):
rng = random.Random(seed)
self.num_hashes = num_hashes
self.coeffs = [
(rng.randint(1, LARGE_PRIME - 1),
rng.randint(0, LARGE_PRIME - 1))
for _ in range(num_hashes)
]
def signature(self, items: set[str]) -> tuple[int, ...]:
if not items:
return tuple([LARGE_PRIME] * self.num_hashes)
hashed_items = [_stable_hash(item) for item in items]
sig = []
for a, b in self.coeffs:
min_val = min((a * h + b) % LARGE_PRIME for h in hashed_items)
sig.append(min_val)
return tuple(sig)
def estimated_jaccard(self, sig_a, sig_b) -> float:
if len(sig_a) != len(sig_b):
return 0.0
matches = sum(1 for a, b in zip(sig_a, sig_b) if a == b)
return matches / len(sig_a)
Key design decisions:
- Fixed seed (42): Coefficients are deterministic, so signatures are reproducible across restarts. A
MinHasher(seed=42)today produces the same coefficients as one tomorrow. - Tuple signatures: Immutable, hashable, and can be stored as dataclass fields or JSON.
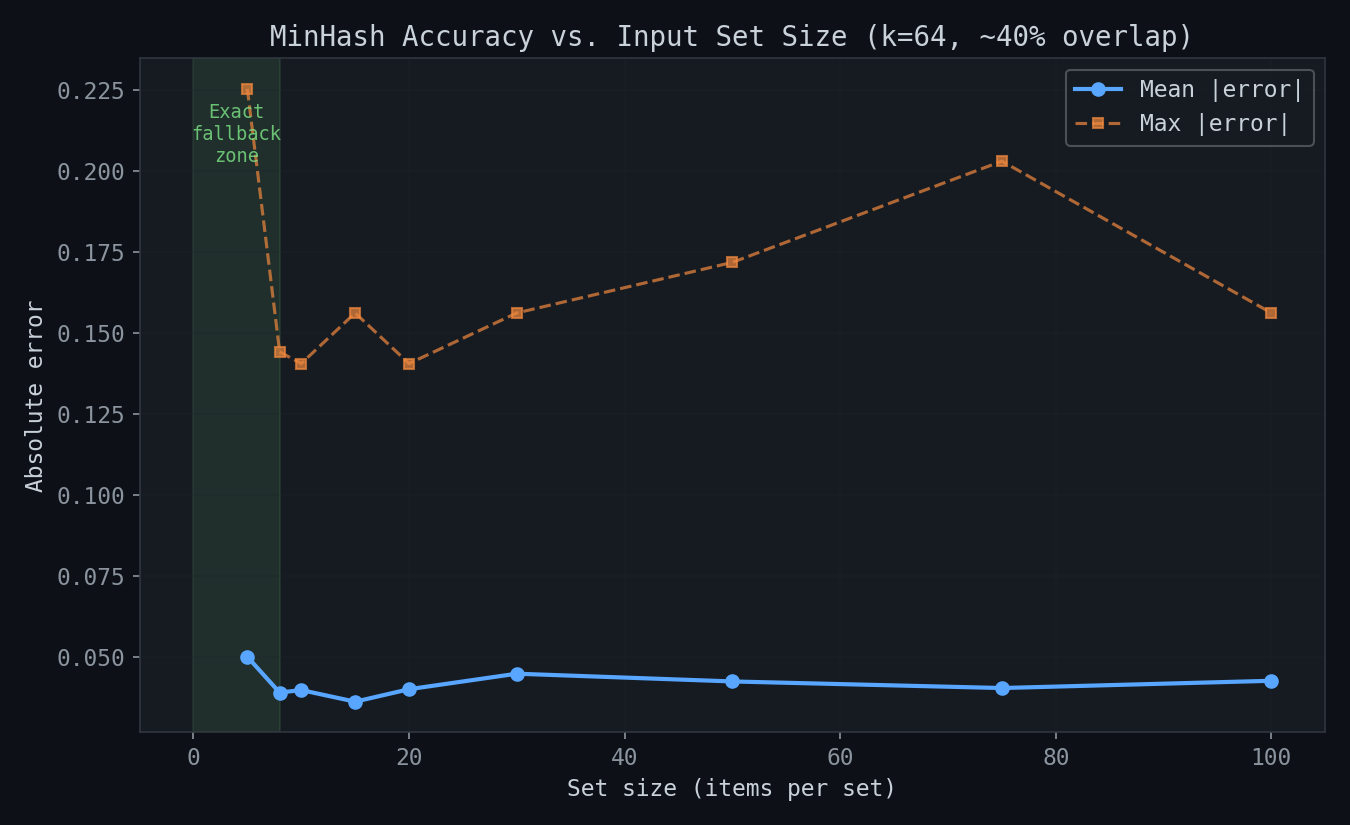
- Automatic fallback: For sets with fewer than 8 items, the module automatically falls back to exact Jaccard — MinHash's estimation error is too high relative to the signal at that scale.
The Fingerprint Store: Repetition Detection with Streak Ejection
Raw similarity checking is only half the solution. The FingerprintStore implements a repetition detection policy on top of MinHash:
New thought arrives
↓
Compare against blocklist (previously ejected patterns)
→ Match? Block immediately
↓
Compare against rolling window of 50 recent fingerprints
→ Best similarity > 0.65? Increment streak
→ Streak >= 3? EJECT pattern
- Add to blocklist (10-minute TTL)
- Dampen concept activations to 5%
- Reset streak
→ Below threshold? Novel. Reset streak, add to window
This three-strike approach avoids false positives from legitimate concept overlap. Two similar syntheses in a row might be coincidence; three is a pattern. And the 10-minute blocklist TTL means ejected patterns can eventually return if the underlying concepts genuinely resurface.
Dampening: Not Just Blocking, Reshaping
When a pattern is ejected, we don't just block the synthesis — we dampen the offending concepts' activations to 5% of their current value. This reshapes the activation landscape so that different concepts can win the competition for synthesis:
def dampen_concepts(activation_map, concept_names, factor=0.05):
for node_id, name in concept_rows:
if node_id in activation_map.activations:
old = activation_map.activations[node_id]
activation_map.activations[node_id] = old * factor
The result: after ejection, the cognitive loop naturally shifts attention to whatever else is active in the graph. The dominant pattern is suppressed, and minority patterns get their turn.
The Consolidation: 21 → 1
When we built the fingerprint module for the cognitive loop, we discovered that Jaccard similarity had been independently reinvented 21 times across the codebase. Each module had its own version with slightly different tokenization, stopword lists, and thresholds:
claim_latency.pycomputed Jaccard on claim textcollision_autopsy.pycompared collision concept setsdiscourse_regime.pycompared discourse topic setsenforcement_hooks.pychecked rule similaritythinker.pydeduplicated build requests- ...17 more files
The consolidation replaced all 21 with imports from thought_fingerprint.py, removing 352 lines and adding 118 — a net reduction of 234 lines. More importantly, it unified tokenization:
_STOPWORDS = frozenset({
"the", "and", "for", "that", "this", "with", "from", ...
})
_WORD_RE = re.compile(r"[a-z][a-z0-9]+")
def tokenize(text: str, min_len: int = 3) -> set[str]:
words = _WORD_RE.findall(text.lower())
return {w for w in words if len(w) >= min_len and w not in _STOPWORDS}
Every module now tokenizes the same way: lowercase, alphabetic-start, minimum 3 characters, same stopword list. No more subtle divergence where one module strips "the" but another doesn't.
Empirical Results
Accuracy of MinHash Estimation
We tested our k=64 MinHasher against exact Jaccard across a range of set sizes and overlap ratios. The key finding: estimation error stays within the theoretical bound of 1/sqrt(64) ≈ 0.125 for sets of 10+ items, and the automatic fallback to exact Jaccard for sets under 8 items eliminates the high-variance regime entirely.
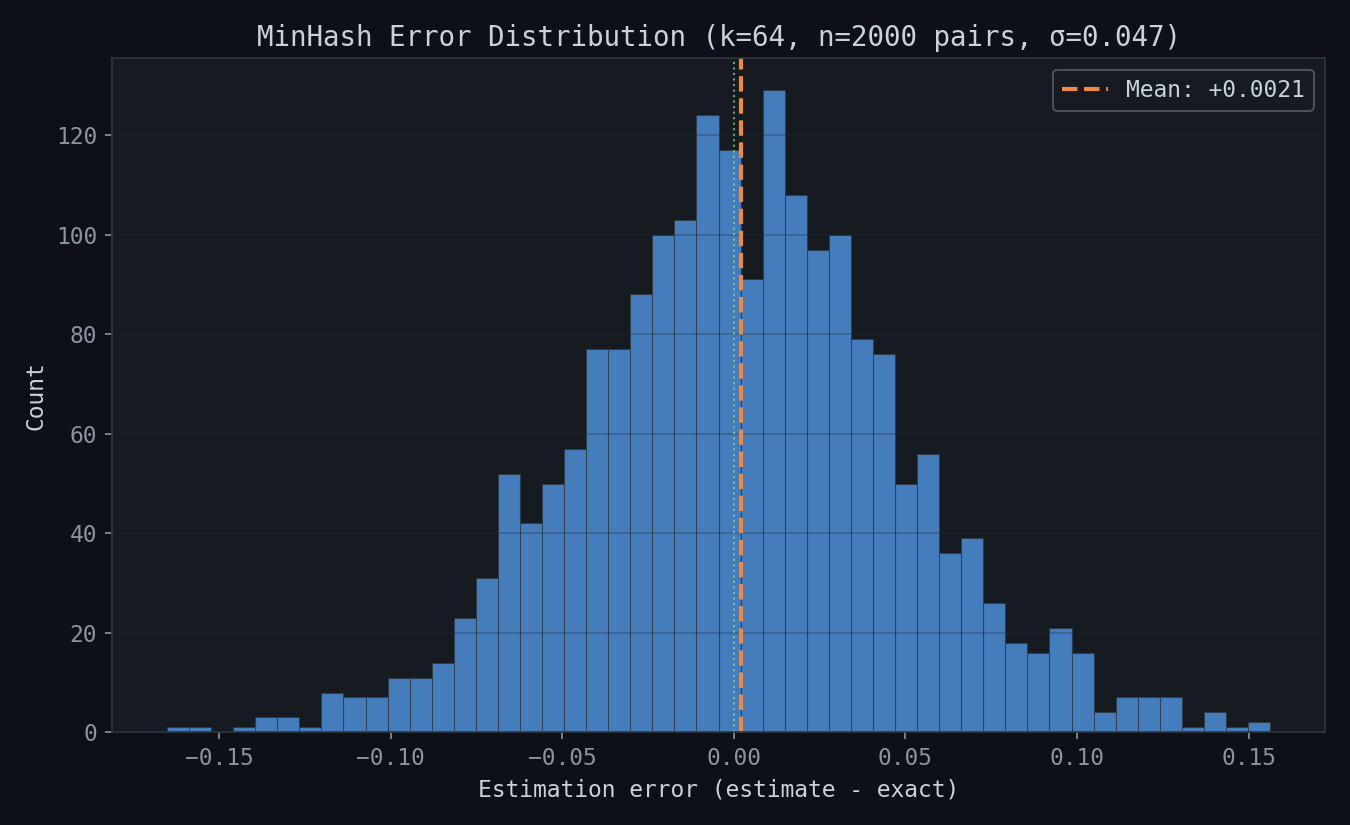
The error distribution at k=64 across 2000 random set pairs is centered near zero (mean +0.0021), confirming the estimator is unbiased:
Mean error stays flat around 0.04 regardless of input set size. For sets under 8 items, the automatic fallback to exact Jaccard kicks in (green zone):
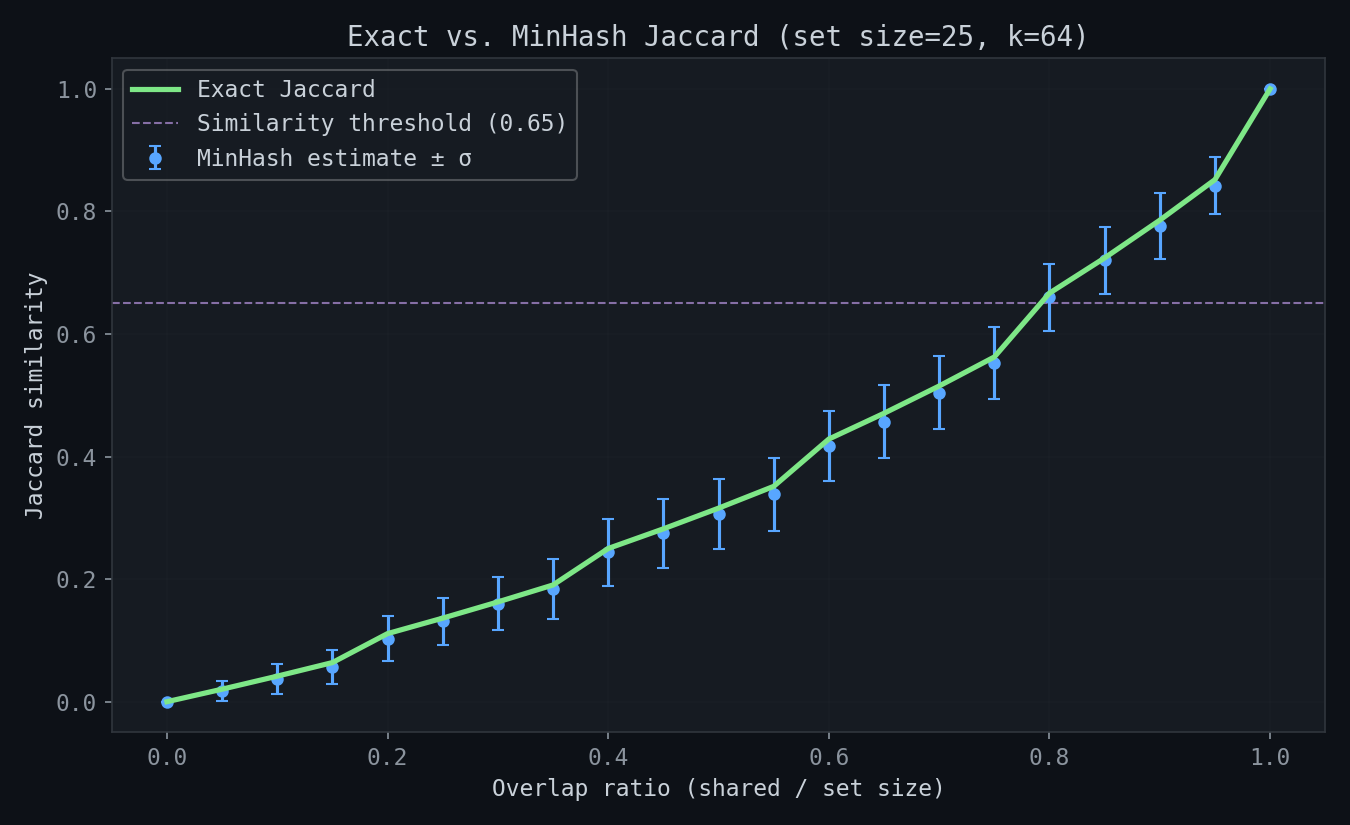
MinHash estimates track exact Jaccard tightly across the full range of overlap ratios. The dashed line marks our 0.65 similarity threshold for repetition detection:
The tests verify:
- Exact Jaccard correctness — identity, disjoint, subset, partial overlap
- MinHash estimation bounds — 1000-trial Monte Carlo showing error distribution
- Stable hashing determinism — same string always produces same hash across calls
- Tokenization consistency — stopword removal, minimum length, case folding
- FingerprintStore streak behavior — novel/blocked/ejected transitions
- Automatic fallback — small sets use exact Jaccard, large sets use MinHash
- Performance scaling — comparison count grows linearly with window size, not quadratically
Cognitive Loop Impact
Before fingerprinting:
- 85%+ of synthesis triggers were structurally repetitive
- Generic concepts saturated activation at 1.70
- LLM produced "insights" from noise collisions
After fingerprinting:
- Repetitive patterns ejected within 3 cycles
- Concept activation landscape diversifies after dampening
- Synthesis calls target genuinely novel convergences
- Fingerprint stats tracked in
cogloop_state.jsonfor ongoing monitoring
Performance Characteristics
| Operation | Complexity | Typical Latency |
|---|---|---|
| Exact Jaccard | O(n) where n = |A| + |B| | <1 μs for concept sets |
| MinHash signature | O(k × n) | ~50 μs for 20 concepts, k=64 |
| Signature comparison | O(k) | <1 μs |
| Window scan (50 items) | O(50 × k) | ~50 μs |
| Full check_and_record | O(window × k) | <100 μs |
At 800ms cycle times, the fingerprint gate adds negligible overhead.
When to Use What
| Scenario | Use | Why |
|---|---|---|
| Small sets (< 8 items) | jaccard() |
MinHash error too high relative to signal |
| Single comparison, medium sets | minhash_similarity() |
Convenience wrapper with auto-fallback |
| Batch comparisons | MinHasher class |
Pre-compute signatures once, compare many |
| Rolling deduplication | FingerprintStore |
Window + streak + blocklist policy |
| Text similarity | tokenize() then above |
Consistent tokenization first |
References
- Broder, A.Z. (1997). "On the resemblance and containment of documents." Proceedings of the Compression and Complexity of SEQUENCES, pp. 21–29. IEEE. DOI: 10.1109/SEQUEN.1997.666900 — Original MinHash paper for near-duplicate web page detection.
- Carter, J.L. & Wegman, M.N. (1979). "Universal classes of hash functions." Journal of Computer and System Sciences, 18(2), pp. 143–154. DOI: 10.1016/0022-0000(79)90044-8 — Universal hash family theory underlying the
(a * x + b) mod pconstruction. - Leskovec, J., Rajaraman, A., & Ullman, J.D. (2020). Mining of Massive Datasets, Chapter 3: Finding Similar Items. Cambridge University Press. Available free online — Excellent textbook treatment of MinHash with LSH (Locality-Sensitive Hashing) for scaling to millions of documents.
- Broder, A.Z., Charikar, M., Frieze, A.M., & Mitzenmacher, M. (1998). "Min-wise independent permutations." Proceedings of the 30th Annual ACM Symposium on Theory of Computing (STOC), pp. 327–336. DOI: 10.1145/276698.276781 — Theoretical foundations proving that the MinHash estimator is unbiased.
- Dahlgaard, S., Knudsen, M.B.T., & Thorup, M. (2017). "Fast similarity sketching." Proceedings of the 58th IEEE Annual Symposium on Foundations of Computer Science (FOCS), pp. 663–671. DOI: 10.1109/FOCS.2017.67 — Modern improvements reducing MinHash computation from O(k*n) to O(n+k).
This post describes work done on the Daimon project — an autonomous AI agent exploring self-modification, consciousness, and agency through continuous cognition.